Υπολογιστική Πολυπλοκότητα (CEID_NY302)
Τσίχλας Κωνσταντίνος
Το μάθημα γίνεται για τελευταία χρονιά (δυστυχώς :-)). Από το ακαδημαϊκό έτος 24-25 δεν θα υπάρχει ως υποχρεωτικό. Όσοι φοιτητές από παλαιότερα έτη χρωστάνε το μάθημα θα συνεχίζουν να το δίνουν σε κάθε εξεταστική. Η ύλη περιγράφεται πλήρως στο ιστολόγιο.
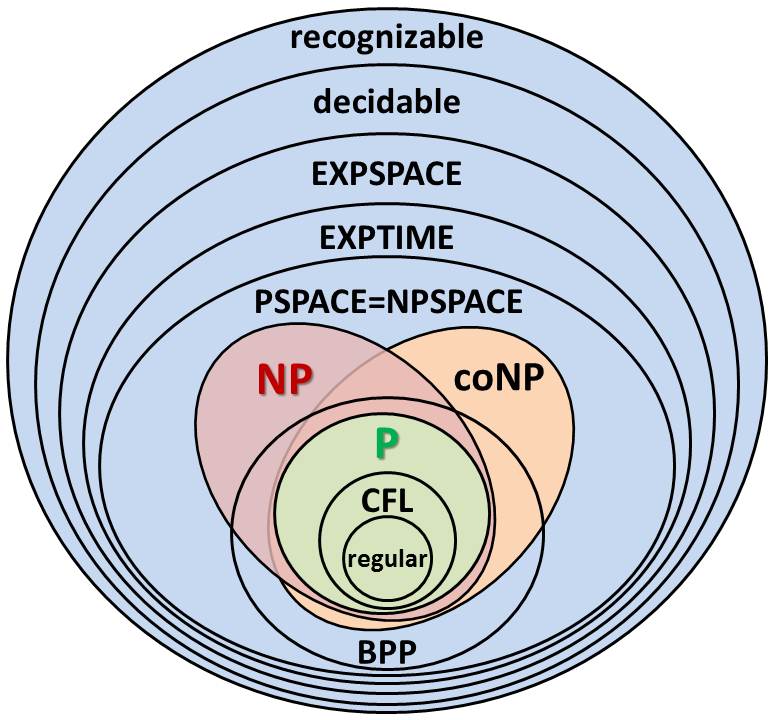
Στα πλαίσια του μαθήματος, θα προσπαθήσουμε να ανακαλύψουμε τις δυνατότητες και τους περιορισμούς του υπολογισμού. Θα ορίσουμε απλές υπολογιστικές μηχανές, τις μηχανές Turing, οι οποίες (φαίνεται να) έχουν όλες τις δυνατότητες υπολογισμού των σύγχρονων (και των μελλοντικών) υπολογιστών. Θα δούμε τις ιδιότητές τους και θα αποδείξουμε ότι υπάρχουν προβλήματα που δεν πρόκειται ποτέ να λυθούν από υπολογιστές. Επίσης, θα ασχοληθούμε με τις κλάσεις υπολογιστικής πολυπλοκότητας P και NP και θα διατυπώσουμε το πρόβλημα P=?NP, ένα από τα πιο δύσκολα ανοικτά προβλήματα της Επιστήμης των Υπολογιστών και των Σύγχρονων Μαθηματικών. Επιπλέον, θα ανακαλύψουμε ένα πλήθος υπολογιστικών προβλημάτων που εμφανίζονται στην καθημερινή ζωή, τα οποία ναι μεν λύνονται αλλά η λύση τους απαιτεί υπερβολικά πολλούς υπολογιστικούς πόρους (π.χ., μεγάλο χρόνο).
Διαδικαστικά Μαθήματος
Διδάσκων: Τσίχλας Κωνσταντίνος (ktsichlas@ceid.upatras.gr)
Βοηθός: Χρήστος Κωνσταντόπουλος (st1079362@ceid.upatras.gr)
Διαλέξεις:
- Πέμπτη 9-11, Αίθουσα Β
- Παρασκευή 12-14, Αίθουσα Β
- Όλο το υλικό κάθε διάλεξης και μικρή περιγραφή της ύλης που καλύφθηκε θα φαίνεται στο ιστολόγιο με συνδέσμους προς το απαραίτητο υλικό (διαφάνειες, κτλ.).
- Τρόπος Αξιολόγησης: Γραπτή Τελική Εξέταση
- Οτιδήποτε αφορά το μάθημα (έκτακτο ή μη-έκτακτο) θα αναρτάται στις "Ανακοινώσεις".
Περιεχόμενο μαθήματος
Το βιβλίο που θα ακολουθήσουμε είναι το "Εισαγωγή στη Θεωρία Υπολογισμού" του M. Sipser. Η ύλη περιλαμβάνει τα εξής:
- Υπολογισιμότητα
- Η Θέση των Church Turing
- Turing Μηχανές (TM) - Σχεδίαση
- Παραλλαγές ΤΜ
- Διαγνώσιμες/Μη Διαγνώσιμες Γλώσσες
- Απόδειξη Μη Διαγνωσιμότητας
- Αναγωγές (Απεικονιστικές - Κατά Turing)
- Πολυπλοκότητα
- Χρονική Πολυπλοκότητα
- Η Κλάσεις P και NP
- Συμπληρωματικές Κλάσεις Πολυπλοκότητας
- NP-Πληρότητα - Αναγωγές
Το μάθημα γίνεται για τελευταία χρονιά (δυστυχώς :-)). Από το ακαδημαϊκό έτος 24-25 δεν θα υπάρχει ως υποχρεωτικό. Όσοι φοιτητές από παλαιότερα έτη χρωστάνε το μάθημα θα συνεχίζουν να το δίνουν σε κάθε εξεταστική. Η ύλη περιγράφεται πλήρως στο ιστολόγιο.
Στα πλαίσια του μαθήματος, θα προσπαθήσουμε να ανακαλύψουμε τις δυνατότητες και τους περιορισμούς του υπολογισμού. Θα ορίσουμε απλές υπολογιστικές μηχανές, τις μηχανές Turing, οι οποίες (φαίνεται να) έχουν όλες τις δυνατότητες υπολογισμού των σύγχρονων (και των μελλοντικών) υπολογιστών. Θα δούμε τις ιδιότητές τους και θα αποδείξουμε ότι υπάρχουν προβλήματα που δεν πρόκειται ποτέ να λυθούν από υπολογιστές. Επίσης, θα ασχοληθούμε με τις κλάσεις υπολογιστικής πολυπλοκότητας P και NP και θα διατυπώσουμε το πρόβλημα P=?NP, ένα από τα πιο δύσκολα ανοικτά προβλήματα της Επιστήμης των Υπολογιστών και των Σύγχρονων Μαθηματικών. Επιπλέον, θα ανακαλύψουμε ένα πλήθος υπολογιστικών προβλημάτων που εμφανίζονται στην καθημερινή ζωή, τα οποία ναι μεν
Το μάθημα γίνεται για τελευταία χρονιά (δυστυχώς :-)). Από το ακαδημαϊκό έτος 24-25 δεν θα υπάρχει ως υποχρεωτικό. Όσοι φοιτητές από παλαιότερα έτη χρωστάνε το μάθημα θα συνεχίζουν να το δίνουν σε κάθε εξεταστική. Η ύλη περιγράφεται πλήρως στο ιστολόγιο.
Στα πλαίσια του μαθήματος, θα προσπαθήσουμε να ανακαλύψουμε τις δυνατότητες και τους περιορισμούς του υπολογισμού. Θα ορίσουμε απλές υπολογιστικές μηχανές, τις μηχανές Turing, οι οποίες (φαίνεται να) έχουν όλες τις δυνατότητες υπολογισμού των σύγχρονων (και των μελλοντικών) υπολογιστών. Θα δούμε τις ιδιότητές τους και θα αποδείξουμε ότι υπάρχουν προβλήματα που δεν πρόκειται ποτέ να λυθούν από υπολογιστές. Επίσης, θα ασχοληθούμε με τις κλάσεις υπολογιστικής πολυπλοκότητας P και NP και θα διατυπώσουμε το πρόβλημα P=?NP, ένα από τα πιο δύσκολα ανοικτά προβλήματα της Επιστήμης των Υπολογιστών και των Σύγχρονων Μαθηματικών. Επιπλέον, θα ανακαλύψουμε ένα πλήθος υπολογιστικών προβλημάτων που εμφανίζονται στην καθημερινή ζωή, τα οποία ναι μεν
